Poker Mavens Statistics Question (3 Viewers)

k9dr · Feb 22, 2021

Can you tell me how often Sicko rivers a straight or flush when I am holding a set or how often the board pairs when I am holding a flush

BearMetal · Feb 22, 2021

k9dr said:
Can you tell me how often Sicko rivers a straight or flush when I am holding a set or how often the board pairs when I am holding a flush

The raw data has this, yes, but parsing the logic and flow behind a hand is considerably more complex.

To be clear, I'm not calling out those moments that you speak of. They are much harder to analyze correctly; that's why I focused on pocket pairs. It's a clean statistic.

k9dr · Feb 22, 2021

BearMetal said:
The raw data has this, yes, but parsing the logic and flow behind a hand is considerably more complex.

To be clear, I'm not calling out those moments that you speak of. They are much harder to analyze correctly; that's why I focused on pocket pairs. It's a clean statistic.

It certainly feels like more often than not

Highli99 · Feb 22, 2021

I am not a maff wizard. I am also not naive about potential nefariance in online poker.

However, when I see a thread about the software being “rigged” my immediate reaction is to think our pattern sensing brains have been again fooled by randomness.

That said, I'm still curious about the math on this will so will follow the discussion.

AWenger · Feb 22, 2021

BearMetal said:
1 table hand = 14 player hands

Only if all 14 players are seated at 1 table.

If it's running 2 tables with 7 players, the hand dealt at Table #1, would be counted separately from the hand dealt at Table #2, in the software, right? Then there are 2 hands, with an average of 7 players per table, for 14 player-hands over 2 table-hands.

How many seats at the final table, when winding down to 1 table? (is it still 7-handed?)

If the tournament starts 7-handed per table, and ends up 2-handed, the average players per hand for the overall tournament would be somewhere in-between.

Just running some numbers in the spreadsheet:
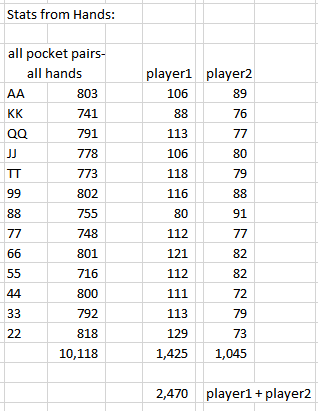
33,662 table-hands multiplied by 5.11 (assumed Average players dealt in per hand), would result in 172,013 Player-Hands, and the average number of pocket pairs expected would be 1 out of 17, or 10,118, which is what is above.

BearMetal · Feb 22, 2021

Jimulacrum said:
It's about 2.5x, not quite 3x. But this is the problem with (relatively) small samples. Does this player's openers represent an average result compared to other players' data? Above average? Below average? Just about every data set is going to have outliers, especially if we're talking about something that's randomized independently every iteration.

In theory, each player should get each pocket pair about an equal number of times as each other pocket pair, which clearly isn't the case here. At the extremes, we have 80 and 129, representing being dealt 22 more than 50% more often than 88. It doesn't mean the site favors 22 or disfavors 88; it's just random variance, like a coin landing on heads a bunch of times in a row. It's a little odd for one player to get an above-average result for all of his pocket pairs, but not any more odd than a player getting a below-average result for all of his pocket pairs, which of course can happen too.

Also, if your hypothesis is that the site is trying to stir up action with unequal hand distributions, shouldn't this pocket-pair data be more top-heavy? Little pairs don't stir up big action; big pairs do. And in this same stroke, I'd like to point out something you addressed right upfront, which is that Briggs has no motive for his software to produce skewed results, whereas he does have motive for it to be fairly randomized. Why should he care if his site stirs up a little more action than others, especially if using broken algorithms to achieve it could drive people away from buying his software?

This is player is one who has played in every tournament. He has the largest single player dataset, so I figured he was a good person to isolate to see if his data aligned. Actually, my point wasn't that the site was trying to use poker rules to stir up fun; it was just that we had noticed an abnormally large number of pocket pairs and when I ran the stats, it seemed to align with that theory.

I guess my point is that Briggs has no reason to do it; the license was paid. Is there a problem with the algorithm? Is there a more general problem? I dunno. I decided to not talk about "fun manufactured hands" specifically because it's much harder to analyze that data (AA vs KK; flop is AKK-A-7l; two huge, aggressive players are in it) ... yes that's fun, but much harder to prove intent of the software. Also, you can say that it's just because you see more hands that you see more scenarios like this. I'm just trying to focus on the simplest raw data to see why it seems pocket pairs come up so often...

Jimulacrum said:
I find it odd that your data on one player includes 9,000+ hands, while your total data pool only covers about 34,000 hands. It makes me feel like you're looking at all of the times all the different pairs have come up across all the players at the table, but still only comparing it to 33,662. If you have 33,662 hands, but 9 players were at the table for each hand, you're really looking at 302,958 openers. Most likely, your data represents somewhat fewer hands than this, since I doubt you're 9-handed all the time, but still way more than 33,662 openers.

Maybe we can test this over a large number of dummy trials. If I understand Mavens (I have a server too but haven't hosted anything yet), you can set up a table that will essentially auto-deal a ton of hands in a relatively short period, without having to involve any real players. Just make two dummy accounts, and make a cash table that's cap-limit Hold'em, with an ante equal to the cap, and duplicate IP addresses allowed. Give both dummy accounts a bazillion chips in their balance and let them buy in for the whole thing. Then just sit them down and let it roll.

In fact, I think I'll take part of my lunch break to see if I can set this up on my server. The part i don't know how to do is run queries on past hands, though, so I may swing back here and ask for help with that.

In this case a 34,000 hands is a table hand; I multiplied by the average number of players to try to normalize the data, but there's still some noise in that data. So, that's why I focused on 1 player with a good dataset.

One thing that seems interesting is that many pocket pair totals are within 2% of one another. Yes, there are outliers, but overall, it feels like there's no real runaway. The vast majority for my single player are in the 100-11x's. The vast majority site-wide are in the upper 700's. So I'm not saying it's skewing it for one pair. But when you account for all of the pocket pairs together over all hands over all players, it seems like it's just too often.

Finest · Feb 22, 2021

Here are the last 90,372 NLHE card pairs dealt on my Mavens site, along with the percentage for each combination and a "1 in" column that indicates that the hand was dealt every 1 in x hands. Pocket pairs are sorted to the top. To be clear, 90,372 is the number of card pairs, not the number of overall "hands" with a variable number of players in each. The average for pocket pairs is 1 in 221 (1/13 x 3/51); the average for non-pairs is 1 in 166 (1/13 x 4/51).

Card 1	Card 2	Pair?	Count	Pct	1 in
2	2	Yes	415	0.46%	218
3	3	Yes	405	0.45%	223
4	4	Yes	405	0.45%	223
5	5	Yes	447	0.49%	202
6	6	Yes	427	0.47%	212
7	7	Yes	404	0.45%	224
8	8	Yes	420	0.46%	215
9	9	Yes	376	0.42%	240
T	T	Yes	436	0.48%	207
J	J	Yes	377	0.42%	240
Q	Q	Yes	418	0.46%	216
K	K	Yes	409	0.45%	221
A	A	Yes	386	0.43%	234
2	3		523	0.58%	173
2	4		569	0.63%	159
2	5		607	0.67%	149
2	6		554	0.61%	163
2	7		590	0.65%	153
2	8		580	0.64%	156
2	9		568	0.63%	159
2	A		554	0.61%	163
2	J		573	0.63%	158
2	K		543	0.60%	166
2	Q		578	0.64%	156
2	T		557	0.62%	162
3	2		572	0.63%	158
3	4		521	0.58%	173
3	5		536	0.59%	169
3	6		533	0.59%	170
3	7		576	0.64%	157
3	8		537	0.59%	168
3	9		524	0.58%	172
3	A		529	0.59%	171
3	J		551	0.61%	164
3	K		558	0.62%	162
3	Q		550	0.61%	164
3	T		553	0.61%	163
4	2		561	0.62%	161
4	3		541	0.60%	167
4	5		534	0.59%	169
4	6		571	0.63%	158
4	7		540	0.60%	167
4	8		524	0.58%	172
4	9		542	0.60%	167
4	A		511	0.57%	177
4	J		538	0.60%	168
4	K		550	0.61%	164
4	Q		531	0.59%	170
4	T		540	0.60%	167
5	2		557	0.62%	162
5	3		535	0.59%	169
5	4		503	0.56%	180
5	6		532	0.59%	170
5	7		526	0.58%	172
5	8		539	0.60%	168
5	9		541	0.60%	167
5	A		566	0.63%	160
5	J		513	0.57%	176
5	K		552	0.61%	164
5	Q		536	0.59%	169
5	T		583	0.65%	155
6	2		544	0.60%	166
6	3		554	0.61%	163
6	4		536	0.59%	169
6	5		528	0.58%	171
6	7		521	0.58%	173
6	8		518	0.57%	174
6	9		546	0.60%	166
6	A		550	0.61%	164
6	J		577	0.64%	157
6	K		577	0.64%	157
6	Q		505	0.56%	179
6	T		537	0.59%	168
7	2		545	0.60%	166
7	3		531	0.59%	170
7	4		552	0.61%	164
7	5		556	0.62%	163
7	6		538	0.60%	168
7	8		533	0.59%	170
7	9		502	0.56%	180
7	A		544	0.60%	166
7	J		518	0.57%	174
7	K		538	0.60%	168
7	Q		500	0.55%	181
7	T		541	0.60%	167
8	2		567	0.63%	159
8	3		492	0.54%	184
8	4		537	0.59%	168
8	5		519	0.57%	174
8	6		536	0.59%	169
8	7		527	0.58%	171
8	9		557	0.62%	162
8	A		564	0.62%	160
8	J		559	0.62%	162
8	K		544	0.60%	166
8	Q		562	0.62%	161
8	T		554	0.61%	163
9	2		549	0.61%	165
9	3		491	0.54%	184
9	4		547	0.61%	165
9	5		519	0.57%	174
9	6		549	0.61%	165
9	7		543	0.60%	166
9	8		548	0.61%	165
9	A		611	0.68%	148
9	J		583	0.65%	155
9	K		509	0.56%	178
9	Q		561	0.62%	161
9	T		560	0.62%	161
A	2		542	0.60%	167
A	3		533	0.59%	170
A	4		558	0.62%	162
A	5		550	0.61%	164
A	6		569	0.63%	159
A	7		561	0.62%	161
A	8		553	0.61%	163
A	9		552	0.61%	164
A	J		538	0.60%	168
A	K		573	0.63%	158
A	Q		536	0.59%	169
A	T		549	0.61%	165
J	2		570	0.63%	159
J	3		571	0.63%	158
J	4		537	0.59%	168
J	5		555	0.61%	163
J	6		549	0.61%	165
J	7		554	0.61%	163
J	8		531	0.59%	170
J	9		556	0.62%	163
J	A		560	0.62%	161
J	K		549	0.61%	165
J	Q		546	0.60%	166
J	T		586	0.65%	154
K	2		533	0.59%	170
K	3		553	0.61%	163
K	4		516	0.57%	175
K	5		522	0.58%	173
K	6		545	0.60%	166
K	7		542	0.60%	167
K	8		541	0.60%	167
K	9		516	0.57%	175
K	A		513	0.57%	176
K	J		504	0.56%	179
K	Q		583	0.65%	155
K	T		565	0.63%	160
Q	2		577	0.64%	157
Q	3		535	0.59%	169
Q	4		540	0.60%	167
Q	5		501	0.55%	180
Q	6		542	0.60%	167
Q	7		528	0.58%	171
Q	8		545	0.60%	166
Q	9		514	0.57%	176
Q	A		555	0.61%	163
Q	J		525	0.58%	172
Q	K		511	0.57%	177
Q	T		561	0.62%	161
T	2		553	0.61%	163
T	3		497	0.55%	182
T	4		548	0.61%	165
T	5		539	0.60%	168
T	6		562	0.62%	161
T	7		616	0.68%	147
T	8		549	0.61%	165
T	9		542	0.60%	167
T	A		532	0.59%	170
T	J		581	0.64%	156
T	K		561	0.62%	161
T	Q		541	0.60%	167

CraigT78 · Feb 22, 2021

shorticus said:
So essentially only the server admin can get access to this information?

Correct. Through either RDP or via the AWS account.

And you've seen your server admin play.

BearMetal · Feb 22, 2021

Highli99 said:
I am not a maff wizard. I am also not naive about potential nefariance in online poker.

However, when I see a thread about the software being “rigged” my immediate reaction is to think our pattern sensing brains have been again fooled by randomness.

That said, I'm still curious about the math on this will so will follow the discussion.

As I said in my OP; I'm the last person to create this thread. I, too, have stood firm with "it's your imagination and because you play so many more hands online than in person". But it's when I ran the stats that I got more curious...

AWenger said:
Only if all 14 players are seated at 1 table.

If it's running 2 tables with 7 players, the hand dealt at Table #1, would be counted separately from the hand dealt at Table #2, in the software, right? Then there are 2 hands, with an average of 7 players per table, for 14 player-hands over 2 table-hands.

How many seats at the final table, when winding down to 1 table? (is it still 7-handed?)

If the tournament starts 7-handed per table, and ends up 2-handed, the average players per hand for the overall tournament would be somewhere in-between.

Just running some numbers in the spreadsheet:
33,662 table-hands multiplied by 5.11 (assumed Average players dealt in per hand), would result in 172,013 Player-Hands, and the average number of pocket pairs expected would be 1 out of 17, or 10,118, which is what is above.

Yes, I know it's not precise turning 2-table tournament hands into player hands. That's why I tried to limit it to a single player as well. If we forget "tournament hands" and focus on player hands, then we get something like this. I picked 2 random players; their percentages for pocket pairs are just way too high!

Player 1 (24,717)
105
111
98
108
90
87
94
79
106
88
94
90
106

Player 2 (15,691)
89
76
77
80
79
88
91
77
82
82
72
79
73

Edit: whoops; pasted wrong total hands

madforpancakes · Feb 22, 2021

Finest said:
Here are the last 90,372 NLHE card pairs dealt on my Mavens site, along with the percentage for each combination and a "1 in" column that indicates that the hand was dealt every 1 in x hands. Pocket pairs are sorted to the top. To be clear, 90,372 is the number of card pairs, not the number of overall "hands" with a variable number of players in each. The average for pocket pairs is 1 in 221 (1/13 x 3/51); the average for non-pairs is 1 in 166 (1/13 x 4/51).

Card 1 Card 2 Pair?
Count
Pct
1 in
2 2 Yes
415
0.46%
218
3 3 Yes
405
0.45%
223
4 4 Yes
405
0.45%
223
5 5 Yes
447
0.49%
202
6 6 Yes
427
0.47%
212
7 7 Yes
404
0.45%
224
8 8 Yes
420
0.46%
215
9 9 Yes
376
0.42%
240
T T Yes
436
0.48%
207
J J Yes
377
0.42%
240
Q Q Yes
418
0.46%
216
K K Yes
409
0.45%
221
A A Yes
386
0.43%
234
2 3
523
0.58%
173
2 4
569
0.63%
159
2 5
607
0.67%
149
2 6
554
0.61%
163
2 7
590
0.65%
153
2 8
580
0.64%
156
2 9
568
0.63%
159
2 A
554
0.61%
163
2 J
573
0.63%
158
2 K
543
0.60%
166
2 Q
578
0.64%
156
2 T
557
0.62%
162
3 2
572
0.63%
158
3 4
521
0.58%
173
3 5
536
0.59%
169
3 6
533
0.59%
170
3 7
576
0.64%
157
3 8
537
0.59%
168
3 9
524
0.58%
172
3 A
529
0.59%
171
3 J
551
0.61%
164
3 K
558
0.62%
162
3 Q
550
0.61%
164
3 T
553
0.61%
163
4 2
561
0.62%
161
4 3
541
0.60%
167
4 5
534
0.59%
169
4 6
571
0.63%
158
4 7
540
0.60%
167
4 8
524
0.58%
172
4 9
542
0.60%
167
4 A
511
0.57%
177
4 J
538
0.60%
168
4 K
550
0.61%
164
4 Q
531
0.59%
170
4 T
540
0.60%
167
5 2
557
0.62%
162
5 3
535
0.59%
169
5 4
503
0.56%
180
5 6
532
0.59%
170
5 7
526
0.58%
172
5 8
539
0.60%
168
5 9
541
0.60%
167
5 A
566
0.63%
160
5 J
513
0.57%
176
5 K
552
0.61%
164
5 Q
536
0.59%
169
5 T
583
0.65%
155
6 2
544
0.60%
166
6 3
554
0.61%
163
6 4
536
0.59%
169
6 5
528
0.58%
171
6 7
521
0.58%
173
6 8
518
0.57%
174
6 9
546
0.60%
166
6 A
550
0.61%
164
6 J
577
0.64%
157
6 K
577
0.64%
157
6 Q
505
0.56%
179
6 T
537
0.59%
168
7 2
545
0.60%
166
7 3
531
0.59%
170
7 4
552
0.61%
164
7 5
556
0.62%
163
7 6
538
0.60%
168
7 8
533
0.59%
170
7 9
502
0.56%
180
7 A
544
0.60%
166
7 J
518
0.57%
174
7 K
538
0.60%
168
7 Q
500
0.55%
181
7 T
541
0.60%
167
8 2
567
0.63%
159
8 3
492
0.54%
184
8 4
537
0.59%
168
8 5
519
0.57%
174
8 6
536
0.59%
169
8 7
527
0.58%
171
8 9
557
0.62%
162
8 A
564
0.62%
160
8 J
559
0.62%
162
8 K
544
0.60%
166
8 Q
562
0.62%
161
8 T
554
0.61%
163
9 2
549
0.61%
165
9 3
491
0.54%
184
9 4
547
0.61%
165
9 5
519
0.57%
174
9 6
549
0.61%
165
9 7
543
0.60%
166
9 8
548
0.61%
165
9 A
611
0.68%
148
9 J
583
0.65%
155
9 K
509
0.56%
178
9 Q
561
0.62%
161
9 T
560
0.62%
161
A 2
542
0.60%
167
A 3
533
0.59%
170
A 4
558
0.62%
162
A 5
550
0.61%
164
A 6
569
0.63%
159
A 7
561
0.62%
161
A 8
553
0.61%
163
A 9
552
0.61%
164
A J
538
0.60%
168
A K
573
0.63%
158
A Q
536
0.59%
169
A T
549
0.61%
165
J 2
570
0.63%
159
J 3
571
0.63%
158
J 4
537
0.59%
168
J 5
555
0.61%
163
J 6
549
0.61%
165
J 7
554
0.61%
163
J 8
531
0.59%
170
J 9
556
0.62%
163
J A
560
0.62%
161
J K
549
0.61%
165
J Q
546
0.60%
166
J T
586
0.65%
154
K 2
533
0.59%
170
K 3
553
0.61%
163
K 4
516
0.57%
175
K 5
522
0.58%
173
K 6
545
0.60%
166
K 7
542
0.60%
167
K 8
541
0.60%
167
K 9
516
0.57%
175
K A
513
0.57%
176
K J
504
0.56%
179
K Q
583
0.65%
155
K T
565
0.63%
160
Q 2
577
0.64%
157
Q 3
535
0.59%
169
Q 4
540
0.60%
167
Q 5
501
0.55%
180
Q 6
542
0.60%
167
Q 7
528
0.58%
171
Q 8
545
0.60%
166
Q 9
514
0.57%
176
Q A
555
0.61%
163
Q J
525
0.58%
172
Q K
511
0.57%
177
Q T
561
0.62%
161
T 2
553
0.61%
163
T 3
497
0.55%
182
T 4
548
0.61%
165
T 5
539
0.60%
168
T 6
562
0.62%
161
T 7
616
0.68%
147
T 8
549
0.61%
165
T 9
542
0.60%
167
T A
532
0.59%
170
T J
581
0.64%
156
T K
561
0.62%
161
T Q
541
0.60%
167

Now that's what I call data!

madforpancakes · Feb 22, 2021

I ran some numbers on my own hand histories, and found the following:

11879 total cash game hands. I only found 30 instances of myself with AA, which multiplied by 221 = 6630. I am usually only in the cash games about half the time they run, so that seems about right to me.

BearMetal · Feb 22, 2021

Finest said:
Here are the last 90,372 NLHE card pairs dealt on my Mavens site, along with the percentage for each combination and a "1 in" column that indicates that the hand was dealt every 1 in x hands. Pocket pairs are sorted to the top. To be clear, 90,372 is the number of card pairs, not the number of overall "hands" with a variable number of players in each. The average for pocket pairs is 1 in 221 (1/13 x 3/51); the average for non-pairs is 1 in 166 (1/13 x 4/51).

Let me try running a similar query on mine ... one moment while I jack-in ...

Finest · Feb 22, 2021

BearMetal said:
one moment while I jack-in ...

View attachment 641656

AWenger · Feb 22, 2021

Something doesn't appear right in the data.

There were 10,118 pocket pairs dealt to all players in all hands. Nothing to question here.

You picked 2 players out of 14 players, and their pocket-pairs totals are 1,425 + 1,045 = total of 2,470. That would be close to 25% of all the pocket pairs dealt in all hands of 10,118. (Or do these 2 often make the final table and cash, and would play 25% of the total hands?)

Somehow I think the data for individual players is not right, or the query for individual players is pulling other unintended data.

BearMetal · Feb 22, 2021

OK, so my site has seen 156,351 unique player hands. If I do a very simply summary here, I get this. This is taking into account some extra games which were not in my original set (play test games for checking cards/chips ... but still, they were hands dealt)

Hands	Occurrences	1-in-x Hands
Total: 156351
AA	827	189
KK	772	203
QQ	811	193
JJ	803	195
TT	799	196
99	820	191
88	783	200
77	777	201
66	826	189
55	739	212
44	826	189
33	805	194
22	830	188

So that's still more often, right? Maybe not as high as my original numbers, but it's happening more often than it should...

Jimulacrum · Feb 22, 2021

BearMetal said:
As I said in my OP; I'm the last person to create this thread. I, too, have stood firm with "it's your imagination and because you play so many more hands online than in person". But it's when I ran the stats that I got more curious...

Yes, I know it's not precise turning 2-table tournament hands into player hands. That's why I tried to limit it to a single player as well. If we forget "tournament hands" and focus on player hands, then we get something like this. I picked 2 random players; their percentages for pocket pairs are just way too high!

Player 1 (24,717)
105
111
98
108
90
87
94
79
106
88
94
90
106
Player 2 (15,691)
89
76
77
80
79
88
91
77
82
82
72
79
73

Edit: whoops; pasted wrong total hands

This data falls much more closely to the theoretical probability of being dealt a pair of whatever.

Player 1 falls a little bit under the curve; a "perfect" data set would have him catching each pocket pair about 112 times out of 24,717 openers. Player 2 falls a little bit above the curve; his "perfect" data would be about 71 of each pocket pair.

The previous sample player you provided has apparently run pretty hot (with openers, anyway) over the tournaments that form your data.

BearMetal · Feb 22, 2021

AWenger said:
You picked 2 players out of 14 players, and their pocket-pairs totals are 1,425 + 1,045 = total of 2,470. That would be close to 25% of all the pocket pairs dealt in all hands of 10,118. (Or do these 2 often make the final table and cash, and would play 25% of the total hands?)

Somehow I think the data for individual players is not right, or the query for individual players is pulling other unintended data.

I chose players who play way more than any other player and they are the most often to cash and have the highest win %. I posted some raw-er stats up above. I guess it makes the data look better (not 5x as often, but still seems too often)...

Jimulacrum · Feb 22, 2021

BearMetal said:
OK, so my site has seen 156,351 unique player hands. If I do a very simply summary here, I get this. This is taking into account some extra games which were not in my original set (play test games for checking cards/chips ... but still, they were hands dealt)

156351 827 189.0580411
772 202.5272021
811 192.7879162
803 194.7085928
799 195.6833542
820 190.6719512
783 199.6819923
777 201.2239382
826 189.2869249
739 211.5710419
826 189.2869249
805 194.2248447
830 188.3746988

So that's still more often, right? Maybe not as high as my original numbers, but it's happening more often than it should...

I mean, yeah, this is still more often than 1 in 221 for each individual pair, but it's just barely off of that theoretical average, well within any reasonable standard of variability. This is worlds different from the first chart you provided.

BearMetal · Feb 22, 2021

Jimulacrum said:
I mean, yeah, this is still more often than 1 in 221 for each individual pair, but it's just barely off of that theoretical average, well within any reasonable standard of variability. This is worlds different from the first chart you provided.

Yup, I agree; it seems as though I just needed to take into account all hands not table hands. Still more often (for every pocket pair) ... but not 5x

k9dr · Feb 22, 2021

Does it matter which seat number they are sitting in - asking for science

Jimulacrum · Feb 22, 2021

I'm running the bot game that I mentioned above just to see, but at the rate it's going, it's only going to deal out about 6,720 hands a day (or 13,440 "player hands" heads-up) which doesn't help a whole lot here. If I can find a way to make it work 9- or 10-handed so that we can get more data, I'll give it a shot. But it seems like we're reaching the point where we realize that the massive discrepancies were likely from data-analysis error and not actually players getting pairs disproportionately often.

If any of you care to check out the bot test, go to the private site Rungood Lounge on Mavens, PW dramaha, cash table RNG Test.

CraigT78 · Feb 22, 2021

k9dr said:
Does it matter which seat number they are sitting in - asking for science

You're still gonna take seat #5.

Because science.

BearMetal · Feb 22, 2021

Jimulacrum said:
I'm running the bot game that I mentioned above just to see, but at the rate it's going, it's only going to deal out about 6,720 hands a day (or 13,440 "player hands" heads-up) which doesn't help a whole lot here. If I can find a way to make it work 9- or 10-handed so that we can get more data, I'll give it a shot. But it seems like we're reaching the point where we realize that the massive discrepancies were likely from data-analysis error and not actually players getting pairs disproportionately often.

Yes, the massive discrepancy was due to analyzing the wrong hand types; but when it switches over to just # of player hands vs # of pocket pairs, it's still too often. Maybe it's within some tolerance, but not 1 of my pocket pairs is above 1-in-221 ... most are in the 180s...

CraigT78 · Feb 22, 2021

Briggs has made his code into a sim where you can run tests.

https://www.briggsoft.com/docs/pmavens/Utilities.htm

Would this help?

Jimulacrum · Feb 22, 2021

BearMetal said:
Yes, the massive discrepancy was due to analyzing the wrong hand types; but when it switches over to just # of player hands vs # of pocket pairs, it's still too often. Maybe it's within some tolerance, but not 1 of my pocket pairs is above 1-in-221 ... most are in the 180s...

What you're seeing in your data isn't really "too often." It's just more often than the theoretical average, but it's not so far off that you'd call it abnormal, especially given the modest sample size.

It's a little odd that all of your pocket pairs are coming in more often than 1 in 221; you'd expect there to be a random smattering of some above and some below that line. But again, not so far off that it should raise any alarms.

BearMetal · Feb 22, 2021

Jimulacrum said:
It's a little odd that all of your pocket pairs are coming in more often than 1 in 221; you'd expect there to be a random smattering of some above and some below that line. But again, not so far off that it should raise any alarms.

Yup, this was my point. After changing the analysis, we're not beyond the realm of theoretical probability for happening too often (at least I don't think we are). But the fact that they ALL are below the 1-in-221 is odd. I guess that's the data that caused myself (and my players) to say "Aren't these freaking PPs coming up too often?"

My OP is updated.

JustinInMN · Feb 22, 2021

Finest said:
Here are the last 90,372 NLHE card pairs dealt on my Mavens site, along with the percentage for each combination and a "1 in" column that indicates that the hand was dealt every 1 in x hands. Pocket pairs are sorted to the top. To be clear, 90,372 is the number of card pairs, not the number of overall "hands" with a variable number of players in each. The average for pocket pairs is 1 in 221 (1/13 x 3/51); the average for non-pairs is 1 in 166 (1/13 x 4/51).

This is the analysis I would have done.

Based on the second data @BearMetal presented it looks like they are getting pairs about 10% more often than expected, but I wouldn't take that alone as a sign something's wrong, I would expect that sort of variance. When we were talking twice-three times as often, I was concerned.

BearMetal · Feb 22, 2021

JustinInMN said:
This is the analysis I would have done.

Based on the second data @BearMetal presented it looks like they are getting pairs about 10% more often than expected, but I wouldn't take that alone as a sign something's wrong, I would expect that sort of variance. When we were talking twice-three times as often, I was concerned.

Yup, that's why I brought it up here. Wanted to get to the bottom of it. Something seemed wrong. Glad we got it straightened out. Still odd they are all happening 10-15% more often ...

Highli99 · Feb 22, 2021

BearMetal said:
Yup, that's why I brought it up here. Wanted to get to the bottom of it. Something seemed wrong. Glad we got it straightened out. Still odd they are all happening 10-15% more often ...

I suspect if you do the analysis exactly like the other one with all hand combos the stats might be a little different. I might be wrong on that but that's my gut.

BearMetal · Feb 22, 2021

Highli99 said:
I suspect if you do the analysis exactly like the other one with all hand combos the stats might be a little different. I might be wrong on that but that's my gut.

I thought that's what I did. I went back and compared the total hands dealt to all players to the number of times we saw pocket pairs.

156351	827	189.0580411
	772	202.5272021
	811	192.7879162
	803	194.7085928
	799	195.6833542
	820	190.6719512
	783	199.6819923
	777	201.2239382
	826	189.2869249
	739	211.5710419
	826	189.2869249
	805	194.2248447
	830	188.3746988

Poker Mavens Statistics Question (3 Viewers)

Royal Flush

4 of a Kind

Royal Flush

Straight Flush

Full House

4 of a Kind

Pair

Royal Flush

4 of a Kind

Straight

Straight

4 of a Kind

Pair

Attachments

Full House

4 of a Kind

Full House

4 of a Kind

Full House

4 of a Kind

Royal Flush

Full House

Royal Flush

4 of a Kind

Royal Flush

Full House

4 of a Kind

4 of a Kind

4 of a Kind

Straight Flush

4 of a Kind