I read it and it is severely flawed. It is comparing 250/500 blinds vs. 250/500 blinds with a 50 ante. That's making an assumption that whomever is making the blind structure simply does away with antes. That is a horrible assumption.
Compare the two structures:
Ante Structure vs. Non-Ante Structure
1. 50/100 vs. 100/200
2. 100/200 vs. 150/300
3. 150/300 vs. 200/400
4. 200/400/50 vs. 300/600
5. 250/500/50 vs. 400/800
6. 300/600/100 vs. 600/1200
Okay, I'll bite, math below. But while you are correct that comparing a 250/500/50 level to a 250/500 level is not an apples-to-apples comparison in terms of orbit cost (250/500/50 has the same per-orbit cost as 400/800 when playing 9-handed), that doesn't make a difference in terms of the basic math of opening ranges. Assuming reasonable stack depth, the math for determining your opening range is the same at 250/500 with no ante as it is at 400/800 with no ante. But I'll treat them as different for the sake of comparison.
Let's assume effective stacks of 20,000 chips, which would be the identical "m" based on per-orbit cost but would be 40 BBs in the ante structure and 25 BBs in the no-ante structure. Assume that it folds to the player in the cutoff.
First, min-raise math with no antes. The cutoff player must raise to 1600 in the no-ante structure to win the 1200 chips in the pot. If the steal works, it gets paid 3:4 (0.75:1). If the BB calls and the cutoff wins at showdown (ignoring postflop action), player wins an additional 800 so would get paid 5:4 (1.25:1). If the button and SB fold, the player in the BB must call 800 to win 2800 (pays 3.5:1, again setting aside postflop play). If the button does call, there is 3600 in the pot, with effective stack of 18,400, a stack-to-pot ratio of about 5.1.
Second, min-raise math with antes. The cutoff player must raise to 1000 in the ante structure to win the 1200 chips in the pot. If the steal works, it gets paid 6:5 (1.2:1). If the BB calls and the cutoff wins at showdown (ignoring postflop action), player wins an additional 500 so would get paid 1.7:1. If the button and SB fold, the player in the BB must call 500 to win 2200 (pays 4.4:1). If the button does call, there is 3200 in the pot, with effective stacks of 19,000, a stack-to-pot ratio of 5.9.
So, in the ante structure at comparable blind levels, the cutoff player gets substantially better odds (60% better, the difference between 1.2:1 and 0.75:1) to try to steal, while the BB also gets better odds (25% better, the difference between 3.5:1 and 4.4:1) to call the raise. Which means there is more incentive to get involved with pots with wider ranges. (I only mentioned the SPR in passing because one could argue that the no-ante structure creates lower stack-to-pot ratio postflop situations and perhaps higher-variance setups.)
I'm not sure you should trust any nonprofessional (and I am very much nonprofessional) to tell you exactly how to construct your ranges differently at those odds. Certainly, these are differences at the margins, not earth-shattering. I might guess that if you would normally open 20% of your hands from the cutoff, an argument could be made that you should open 32% instead (a 60% larger range). Of course, there are spillover effects from that, like if the Button knows the cutoff is opening 32% of hands the button should 3-bet a wider range. That's poker, you can't do the math in a vacuum.

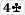
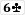 becomes an open shove!
becomes an open shove!