Hand Analysis - Before it Airs (2 Viewers)

[boltonguy]

I maxed out the turn bet at 75% pot but we see that the solver is preferring the this size with Brynn's hand

 

[boltonguy]

77 is again a pure call:

 

[Senzrock]

77 is again a pure call:

View attachment 914043

Just as I expected so far - although Brynn’s flop bet sizing is very interesting!

 

[bergs]

GTO might be the single dumbest thing in poker since…

“Hey can you wash the cards?”
“Thanks for the river 3s dealer!”
“ONE TIME”
“Can we get a new setup?”

Actually, ONE TIME is pretty great properly used.

 

[bergs]

I haven't used solvers either, so perhaps I'm not the best to answer your practical question. But as a matter of theory - the right way to play against an opponent depends on how he plays.

Say you're holding QJs, you open, and villain 3-bets. If he only 3-bets with AA, KK, and AK then your optimal strategy is to fold (I'm simplifying here). If instead he 3-bets with any pairs and any broadway then your optimal strategy is to call. So your optimal strategy depends on his range, which is to say, on his strategy. So the answer to the question "are we not able to plug in just our holdings into the solver vs a range and see how we “should” proceed" is NO, unless you know what his strategy is and can provide it to the solver.

Now, you can just plug in a single hand and have the solver tell you how you should play, but that only works because the solver assigns a default strategy to the villain and assumes that the villain is using that strategy, and therefore the solver can tell you what your optimal play is given your holding and given villain's assumed default strategy.

... and what is that default strategy that the solver assumes the villain is using? Why, it's GTO.

So if your opponent is playing GTO, then the solver will tell you your best play. But if your opponent is NOT playing GTO, then in order to tell you your best play, you'll need to tell the solver what strategy your opponent IS using, and you can do that by specifying the villain's range.

BUT WAIT! That's not enough either, because your opponent's strategy doesn't merely consist of his range, but also of how he will react to your plays, and that in turn depends on what he perceives your strategy is. So to accurately predict how your opponent will play, the solver also needs to know your range, or, more precisely, what your opponent thinks your range is. Which is why @boltonguy wanted to try to construct ranges for Krish and Kenney; GTO solvers are accurate if the players are playing GTO, but less so if they aren't, unless you take the extra steps to specify what their actual strategy is. The players here are so far from GTO that asking what PIO recommends "by default" in this spot isn't especially helpful; it would recommend something that would be much less profitable in this actual situation with these two actual players than it could be.

Please show me my range if I’m playing BDT.

 

[Windwalker]

77 is again a pure call:

View attachment 914043

Still trying to understand this, but according to the solver, it favors a call against a fold or raise on the turn, yes? Raise is 9.8%, call is 52% and the rest is fold?

 

[davislane]

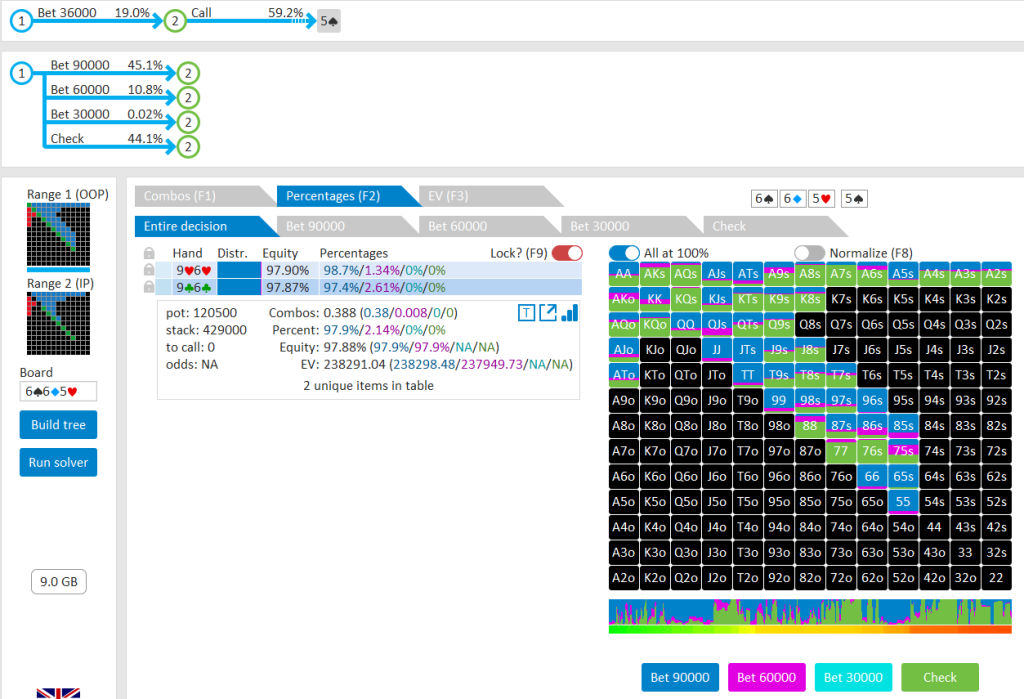
Still trying to understand this, but according to the solver, it favors a call against a fold or raise on the turn, yes? Raise is 9.8%, call is 52% and the rest is fold?

Yes. Your raise was the correct play ~1 in 10 times. So the next 5 times you find yourself in a similar situation you should call and the other 4 fold. Thankfully for you that 1 in 10 situation worked out.

The thing with solvers, is they give you a frequency of different options. One really needs to be using an RNG to decide when to do the various options to maximize the benefit of solvers.

 

[Senzrock]

Still trying to understand this, but according to the solver, it favors a call against a fold or raise on the turn, yes? Raise is 9.8%, call is 52% and the rest is fold?

Exactly. We should most often be calling, but a fold isn’t terrible as solver notes we will often be behind in this spot (true in this case also), and the under 10% raise shows us how little we want to take an aggressive action here.

 

[boltonguy]

@Windwalker The stats that you put in your post (9.8% raise, 52% call and 38.2% fold) are the frequencies for your entire range in aggregate as displayed in the range chart. Below I have selected your exact hand and 77 is a 100% call in this solve. So the solver will never raise or fold this exact hand to a bet of this sizing, only call.

It shows your exact hand having 48% equity versus V's range (as defined in the solver for V's range - this is a solver input that we create). So I think that with almost 50% equity we're never folding (which would give up a ton of equity) but not raising for value (as V is uncapped and has AA, KK, QQ as well as the strongest combos with 5x and 6x), and we're not turning our overpair into a bluff here as we have SDV.

 

[Frogzilla]

The solver has Brynn favoring the 125% flop sizing overall and with his specific hand.

View attachment 914037

I think this means need to adjust PF ranges…too much 6x nut advantage as input for BK. Can you do mixed freqs for the suited 2/3 callers? And add in some 56s, 67s, 78s for krish at mixed freq?

 

[Senzrock]

I think this means need to adjust PF ranges…too much 6x nut advantage as input for BK. Can you do mixed freqs for the suited 2/3 callers? And add in some 56s, 67s, 78s for krish at mixed freq?

Good point, except I don't know if Krish is raise-calling those combos UTG for $7k/$20k right? I think our range is pretty solid.

 

[CrazyEddie]

Still trying to understand this, but according to the solver, it favors a call against a fold or raise on the turn, yes? Raise is 9.8%, call is 52% and the rest is fold?

It's easy to misunderstand what the solver's output means, and it's worth taking the time to properly understand it.

Solvers produce what game theorists call a mixed strategy. The opposite of a mixed strategy is a pure strategy. A pure strategy is one that you might use in a full-information deterministic game such as chess; such a strategy might look like "If he plays E4 then I'll reply with C5; if instead he plays D4 then I'll reply with D5." In a pure strategy, every time it's your turn there will be exactly one move that you will always make in the particular situation you are in.

Mixed strategies are used for games with hidden information and randomized outcomes, such as poker. In a mixed strategy, for any given situation, when it's your turn, there will be multiple different moves that the strategy will say you should make. The strategy will tell you a probability distribution among those moves, like "Call 50%, Raise small 30%, Raise big 20%, Fold 0%".

Given the probability distribution that the strategy tells you to use, you should randomly choose between those different possible moves, weighting the random selection between them according to what the strategy specifies.

This last bit is important, and often misunderstood. The percentages that a solver provides aren't how much the solver likes each different move - the solver likes all the specified moves equally. Every one of the specified moves has the same EV, and that EV is the maximum EV that can be obtained in that situation. The moves that the solver assigns 0% probability to all have a smaller EV and have been excluded from the allowed moves. So in a given situation, as long as you choose any of the non-zero probability moves that the solver offers, you have played optimally. They will all produce the same result on average, which is what EV is.

So if the percentages aren't how much the solver likes each move, what are they? They are the weights you should use in choosing between them randomly - not because some are better than the others, but merely because if you don't choose randomly between them and do so with the specified weights then your opponents will, over time, be able to read your hands and predict your choices. The probabilities are there not to pick the best move but to disguise your play. They're only relevant across multiple hands, against opponents who can observe your habits and draw inferences about your tendencies. The probabilities are there to ensure you have no tendencies for them to draw inferences about.

 

[boltonguy]

Well I think for his overall range he is favoring this larger size as well:

Dark blue is the larger size:

All the 6x and many bluffs (suited broadways and gappers). Probably because Krish opening and calling the 3! gives him a pretty condensed range which misses this board and is absent the strongest overpairs so fire away to either get value or a fold based on Krish's exact holding!

 

[Senzrock]

The percentages that a solver provides aren't how much the solver likes each different move - the solver likes all the specified moves equally.

I liked your explanation, but this sentence can be pretty confusing to most. When a solver give us 50% for one action and 10% for another action, to say that the solver likes them equally can feel a bit misleading in practice. But yes, the point is how often you "should" be taking each action, not what is the exact action that you should be taking in that spot every time. However, for those that don't use solvers, the %'s are still good indicators of what you "should" be doing, assuming they are not using a randomizer while they play. Also, as you point out, solvers are really directed towards professionals who are seeking perfect "or as close to perfect as is possible" balance in their play over a large sample size. In this real world example, Krish may never play another hand vs Brynn in his entire life so exploitative play should be prioritized.

 

[bergs]

Give me 3 pitchers of margaritas, I’ll give ya a fuckin’ solvah you dirty ingrates.

 

[CrazyEddie]

I liked your explanation, but this sentence can be pretty confusing to most. When a solver give us 50% for one action and 10% for another action, to say that the solver likes them equally can feel a bit misleading in practice.

It's difficult to reason about game theory, GTO, and solvers, and even more difficult to talk precisely about them. What they do runs counter to human intuition and runs past our ability to understand the details. So I agree, some of what I said there can be misleading.

If a solver presents more than one move at greater than 0% probability, all of those moves have the same EV - given that the solver's model of both players' strategies from that point onward is accurate. The solvers model perfect play using whatever perfect or imperfect strategies the user has assigned to the players... but of course not only do players not use perfect strategies, they don't even perfectly play their imperfect strategies. Furthermore, human players use metastrategies that solvers don't take into account; if I think that you've been playing tight and value betting the river all night long but I think that now at the end of the night you're getting tired and swingy and will totally bluff with air, and I came to this conclusion halfway through the current hand, then my strategy will change midhand to react to my perceived change in your strategy. Solvers have no good way to account for this sort of play.

So the solver's 10% and 50% solutions can be considered equivalent, in that they both have the same EV - under idealized circumstances which almost certainly don't exist.

But yes, the point is how often you "should" be taking each action, not what is the exact action that you should be taking in that spot every time. However, for those that don't use solvers, the %'s are still good indicators of what you "should" be doing, assuming they are not using a randomizer while they play. Also, as you point out, solvers are really directed towards professionals who are seeking perfect "or as close to perfect as is possible" balance in their play over a large sample size. In this real world example, Krish may never play another hand vs Brynn in his entire life so exploitative play should be prioritized.

I'd go so far as to say that any tendencies you can actually observe in your opponents should be exploited 100% of the time, even at the risk of creating tendencies that themselves could be counter-exploited. The theoretical models that solvers deal with take hundreds of thousands of hands to reveal or detect minor deviations from perfect play, because it's entirely a matter of statistics; no one play, or even a handful of plays, is enough to say "A HA! That's an exploitable deviation, he folds 40% too frequently when facing a 3-bet with less than a suited broadway hand!" The solvers take this level of detail into account when constructing their strategies because they play millions (billions?) of hands against themselves.

No human is capable of such thinking. They can't spot tendencies because they don't observe enough hands, don't play enough hands, and can't perform that degree of analysis. Likewise, they can't avoid tendencies when constructing their strategies; at best they can do a crude approximation which we laughingly call "balanced". Which is why my advice to human players at any level is - try to play balanced but don't obsess about it; you're doing a bad job at it but it's probably good enough; and if you play against someone who you think isn't balanced then try to exploit the f*** out of them 100% of the time even if that makes you unbalanced because they'll never even notice.

I'm not certain whether the play with the highest percentage from a solver always corresponds to the maximally exploitive play, though, so I can't say with confidence that the highest percentage play is always the best play. At the very least, though, it's not bad. Solver solutions are never bad. Not very bad, anyway.

 

[Senzrock]

I'm not certain whether the play with the highest percentage from a solver always corresponds to the maximally exploitive play, though, so I can't say with confidence that the highest percentage play is always the best play

Yeah I imagine this would be difficult to ascertain, although with a few live reads/factors (in this case we know that Brynn was stuck a decent amount, at the end of a session, was looking to play hands with hero and in general is an aggressive villain), we can make some pretty strong education guesses. So the call on the turn for example just seems "best", given both what we know in game but also looking back at what the solver is showing us.

 

[bergs]

So what’s the point of a solver and GTO in general for people that play only live and aren’t going to face a particular situation hundreds of thousands of times?

Honestly the whole GTO thing just seems like an angle for poker coaches to get money by teaching this “new unbeatable mathematics based strategy”.

 

[Senzrock]

So what’s the point of a solver and GTO in general for people that play only live and aren’t going to face a particular situation hundreds of thousands of times?

Honestly the whole GTO thing just seems like an angle for poker coaches to get money by teaching this “new unbeatable mathematics based strategy”.

I know you have been mostly trolling so far but, assuming this is a serious question, a solver can "teach" us how to strive for a more balanced strategy long term. This will actually be the most profitable strategy for us, even though we can never achieve "perfect balance." See, in order to deviate from a balanced strategy (to play an exploitative strategy), we first have to understand what a balanced strategy means. When we raise every flop with a strong hand, that will get picked up on at almost any game we play, even a $1/2 live game. We know, even without solvers, that we want to mix up our play here and there so that occasionally we trap with strong hands and occasionally we fast-play them, that just makes sense right? A solver can show you the ideal frequencies of a given play, taking into account stack depth and perceived ranges (perceived ranges can be quite complicated as well, but you can definitely approximate them so that they will be useful to you).

But beyond the question of "should we check-raise the flop every time we hit a set or not" a solver can also show us frequencies for continuing with certain holdings in certain spots, which can illuminate new decision making strategies for us in ways that we might not have understood before. A solver might tell us that, given our hand in a certain spot (let's say one over card and a backdoor flush draw), that we should be calling a lot more check-raises on a certain flop texture than maybe we thought. So it can show us that we are over-folding in certain instances in ways that might be counterintuitive to us.

Just because no one can play truly GTO or balanced, doesn't mean that these are not great concepts that will help us improve our game. Poker is an amazingly complex game that you can dive as deep into as you want, and solvers help us do that. Now many players (maybe such as yourself, I don't know), are not interested in digging into deeper strategies of the game, and that's totally understandable. But others are, especially those who's financial status depends on deepening their understanding of optimal strategies.

Is that helpful?

 

[horseshoez]

After some thorough analysis,

Good chance we’ll be seeing the following in the future,

 

[bergs]

I know you have been mostly trolling so far but, assuming this is a serious question, a solver can "teach" us how to strive for a more balanced strategy long term. This will actually be the most profitable strategy for us, even though we can never achieve "perfect balance." See, in order to deviate from a balanced strategy (to play an exploitative strategy), we first have to understand what a balanced strategy means. When we raise every flop with a strong hand, that will get picked up on at almost any game we play, even a $1/2 live game. We know, even without solvers, that we want to mix up our play here and there so that occasionally we trap with strong hands and occasionally we fast-play them, that just makes sense right? A solver can show you the ideal frequencies of a given play, taking into account stack depth and perceived ranges (perceived ranges can be quite complicated as well, but you can definitely approximate them so that they will be useful to you).

But beyond the question of "should we check-raise the flop every time we hit a set or not" a solver can also show us frequencies for continuing with certain holdings in certain spots, which can illuminate new decision making strategies for us in ways that we might not have understood before. A solver might tell us that, given our hand in a certain spot (let's say one over card and a backdoor flush draw), that we should be calling a lot more check-raises on a certain flop texture than maybe we thought. So it can show us that we are over-folding in certain instances in ways that might be counterintuitive to us.

Just because no one can play truly GTO or balanced, doesn't mean that these are not great concepts that will help us improve our game. Poker is an amazingly complex game that you can dive as deep into as you want, and solvers help us do that. Now many players (maybe such as yourself, I don't know), are not interested in digging into deeper strategies of the game, and that's totally understandable. But others are, especially those who's financial status depends on deepening their understanding of optimal strategies.

Is that helpful?

I guess I get it if retroactively applied to situations you may encounter frequently where you’re not sure if you made the right play - normally on draws I’d imagine. I don’t see the point much with gaming out a super specific situation like 77 with that board texture but I’m not at all a math guy.

 

[CrazyEddie]

I guess I get it if retroactively applied to situations you may encounter frequently where you’re not sure if you made the right play - normally on draws I’d imagine. I don’t see the point much with gaming out a super specific situation like 77 with that board texture but I’m not at all a math guy.

Think of it like this. There's a book titled "How To Play Perfect Poker". It comes in several volumes, and it looks like this:

You get to read as much of it as you like, and for every page you study and remember, you'll be unbeatable at poker in that specific situation.

Obviously at first you want to study the sections that come up the most often. But there's some value in skimming through the other pages throughout the entire bookshelf, so that you can maybe build up a better sense of how to handle situations that you haven't encountered before when they do come up, even if they don't come up very often.

Studying with solvers is about choosing which of those volumes to read, and how much time to spend on each volume.

 

[Legend5555]

The thing over learned most from my limited exposure to solvers is how to determine good hands to bluff with vs bad hands to bluff with. It really illuminates why blockers matter. Even though blocker effects can be considered minor, they are good way of determining what makes the difference between bluffing or not and hero calling or not.