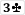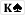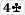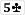Who wins? (1 Viewer)

[BGinGA]

Chip race in tourney too

Plus first-to-act in stud games.

 

[JustinInMN]

I guess the pot could be like $1.75, or 7 quarters, so the high and low would each get 75¢, with the odd 25¢ going to the high, and then the 75¢ for the low would need to be split again. In which case, we might have done 75¢ to the high, and 50¢/50¢ for the quartered low (rather than $1 to the high and only 25¢/25¢ for the quartered low).

you could have a total pot of 11 chips split between 1 high and 2 lows - if 6 goes to high (high gets first odd chip), then 5 gets split between the lows and now you have 2+2 and another odd chip... ?

The correct way is both of these cases is the pot is split in two and an odd chip is awarded to the high. If that leaves an odd number of chips in the low half that needs to be split again, that's just the breaks.

All that said, you'll notice the pots in these examples are extremely small. Meaning no players were betting with any real expectation anyway. If @TheOffalo 's example is 25¢-50¢ blinds then this is the smallest pot possible with an odd number of chips and 3 players to receive some portion at showdown. One of the low players effectively gets their money back, the low player with better position gets half their money back, and the high player get the small blind plus one chip from the low player with better position. Considering no one was betting their hands, and everyone got something back when no one was expecting to win, and again, this is about the "worst" case scenario in terms of pot size and odd chips, I am fine with this result if the alternative is introducing complicated exceptions to cover these rare scenarios.

You could make a house rule to get around this, but it's probably not worth the added confusion of reconstructing high and low pots once the exception has been identified. Even a rule like "ensure an even number of chips go to the side of the pot to split two ways" addresses one specific scenario, but does not cover the myriad of scenarios introduced by possible 3- and 4-way chops on either side of the pot. The simple rule is probably better even if this gets quirky in small pots.

However, most pots that need to be split will be of higher value and the odd chips will largely go unnoticed. A pot with $19.75 (about an average size for a 25¢-50¢ blind game, ymmv of course) for example in a similar scenario would put $10.00 in the high pot, and the low pot would be split $5.00 and $4.75. This being the more frequent scenario, a complicated exception to the rule to accommodate the extremely rare chopping of small pots is probably unnecessary.

 

[TheOffalo]

Very well reasoned @JustinInMN, thanks for the feedback/sanity check!

 

[JustinInMN]

Yes but 1 and 3 both have the seemingly irrelevant so result is fouled deck, all bets returned

Very well played .

 

[JustinInMN]

The correct way is both of these cases is the pot is split in two and an odd chip is awarded to the high. If that leaves an odd number of chips in the low half that needs to be split again, that's just the breaks.

All that said, you'll notice the pots in these examples are extremely small. Meaning no players were betting with any real expectation anyway. If @TheOffalo 's example is 25¢-50¢ blinds then this is the smallest pot possible with an odd number of chips and 3 players to receive some portion at showdown. One of the low players effectively gets their money back, the low player with better position gets half their money back, and the high player get the small blind plus one chip from the low player with better position. Considering no one was betting their hands, and everyone got something back when no one was expecting to win, and again, this is about the "worst" case scenario in terms of pot size and odd chips, I am fine with this result if the alternative is introducing complicated exceptions to cover these rare scenarios.

You could make a house rule to get around this, but it's probably not worth the added confusion of reconstructing high and low pots once the exception has been identified. Even a rule like "ensure an even number of chips go to the side of the pot to split two ways" addresses one specific scenario, but does not cover the myriad of scenarios introduced by possible 3- and 4-way chops on either side of the pot. The simple rule is probably better even if this gets quirky in small pots.

However, most pots that need to be split will be of higher value and the odd chips will largely go unnoticed. A pot with $19.75 (about an average size for a 25¢-50¢ blind game, ymmv of course) for example in a similar scenario would put $10.00 in the high pot, and the low pot would be split $5.00 and $4.75. This being the more frequent scenario, a complicated exception to the rule to accommodate the extremely rare chopping of small pots is probably unnecessary.

Another approach, we just round the half pots down and drop the remainder, into an account we opened.

 

[BGinGA]

One game I used to deal, the house rule was that all odd chips went to the dealer. I liked that rule.

 

[TheOffalo]

We’ve given the odd chip to the host before.

 

[isthisevencreative]

Will this got all off topic...

Please let the OP answer this before chiming in.

Little Hold Em quiz for @isthisevencreative :

Question 1:

Player 1:
Player 2:

Final board:

Who wins?


Question 2:

Player 1:
Player 2:

Final board:

Who wins?


Question 3:

Player 1:
Player 2:

Final board:

Who wins?


Question 4:

Player 1:
Player 2:

Final board:

Who wins?

Q1: players split
Q2: players split
Q3: players split
Q4: players split
Not entirely sure if I got them all correct but after watching some YouTube videos i think I did

 

[TheOffalo]

Q1: players split
Q2: players split
Q3: players split
Q4: players split
Not entirely sure if I got them all correct but after watching some YouTube videos i think I did

Yes, No, Yes, No.

 

[isthisevencreative]

Yes, No, Yes, No.

How so? Please explain

 

[TheOffalo]

How so? Please explain

Question 1:

Player 1:
Player 2:

Final board:

Who wins?

You're correct it's a chop because both players have

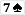
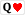
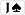
Question 2:

Player 1:
Player 2:

Final board:

Who wins?

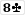
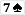
Player 2 wins because his (or her) winning hand is 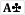while Player 1's hand is

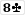
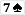
Question 3:

Player 1:
Player 2:

Final board:

Who wins?

You're correct it's a chop because both players play the board:

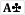
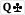
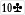
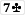
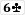
Question 4:

Player 1:
Player 2:

Final board:

Who wins?

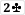
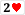
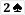
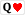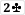
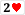
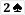
Player 1's hand is , while Player 2 has , so Player 1 wins.

 

[BGinGA]

How so? Please explain

Answers below in bold.

Will this got all off topic...

Please let the OP answer this before chiming in.

Little Hold Em quiz for @isthisevencreative :

Question 1:

Player 1:
Player 2:

Final board:

Who wins?
chop -- both players have 77AQJ

Question 2:

Player 1:
Player 2:

Final board:

Who wins?
P2 wins with 8877A vs 88776

Question 3:

Player 1:
Player 2:

Final board:

Who wins?
chop - both players have club flush with AQT76

Question 4:

Player 1:
Player 2:

Final board:

Who wins?
P1 wins with 2222Q vs 2222J

 

[TheOffalo]

Answers below in bold.

Jinx!

 

[OfficerLovejoy]

How so? Please explain

The answer is always: the best possible 5 card hand out of the 7 cards available wins. If that happens to be the same hand for two or more players, the pot is split between the players still in the hand.

 

[isthisevencreative]

Jinx!

You're correct it's a chop because both players have



Player 2 wins because his (or her) winning hand is while Player 1's hand is




You're correct it's a chop because both players play the board:



Player 1's hand is , while Player 2 has , so Player 1 wins.

Ooooo ok thank you I was kinda comfused

 

[JustinInMN]

Ooooo ok thank you I was kinda comfused

Always looking for the best 5 cards. What happened in Question 2 you might hear called "counterfitting." Basically even though Player 1 has a pair in his hand, it's value is reduced on this board because because there are two higher pairs on the board that are available to everyone. Since neither player has an 8, a 7, a pair 77 or greater, or 22, the only way to improve on the board is players using one card to replace the Player 2's best card for this is an Ace, Player 1's best card is either of the sixes.

When you are learning hold'em, one of the best exercises is to practice reading five card boards and figuring out the best possible hole cards to make the best possible five card hands. In Question 4, for example, with quads on the board, the best possible hole card to have is any Ace. (Four of a kind deuces with an ace kicker.) After that is any king (Four of a kind deuces with a king kicker), and then Player 1's holding, any queen (Four of a kind deuces with a queen kicker)

In question 2, the best possible hole cards are as follows: 88 (four of a kind, eights), 77 (four of a kind, sevens), Any single eight (eights full of sevens), Any single seven (sevens full of eights), 22 (deuces full of eights), AA (two pair, aces and eights, or "aces-up"), KK (two pair, kings-up), and the other pocket pairs down to 99 all make two pairs with the 88 on board, then Any single Ace (two pair, eights and sevens, or "eights-up" with an ace Kicker, this is player 1's holding)

 

[Beakertwang]

Just wait till the OP tries to figure out Omaha hi/lo.

 

[isthisevencreative]

Just wait till the OP tries to figure out Omaha hi/lo.

Nah what not be for a while

 

[TheSalt]

Just wait till the OP tries to figure out Omaha hi/lo.

Or a variant like 2-7 triple draw