How can this possibly be right?
I think I get what solvers do and I think I understand the point of GTO play, but I find it maddening so I don't really know much about it.
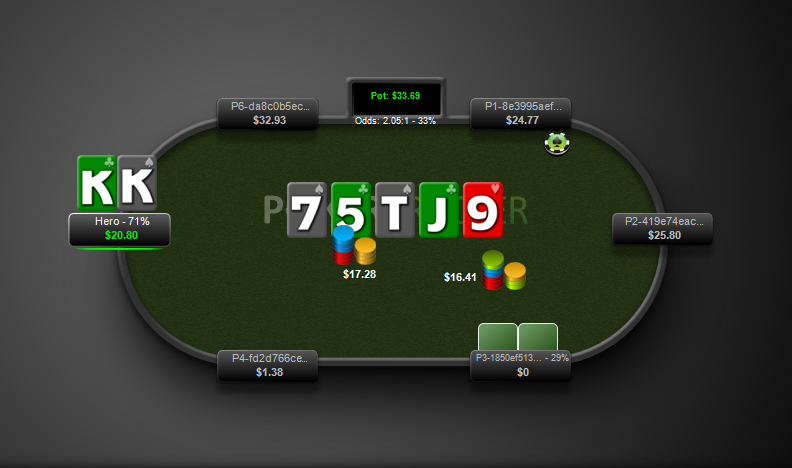
But how can it tell you that GTO play is to jam that river 100% of the time? When V is literally ALWAYS behind here?
EDIT - I suppose the answer is that the solver knows Heros are folding more than 50% of the time here? is that it? If you know you're going to win at least 51% of the time, it's profitable to jam every time?
I'll try but please keep in mind that I'm still learning this and am far from expert so I may be right, wrong or close. Happy to be corrected by the experts.
In GTO, both players have perfect knowledge of each other's strategies; they know in every spot exactly how their opponent will play every combo in their range and at what frequencies. In a specific spot, laying specific odds, Villain's goal is to balance bluffs and value bets across combos in her range so that Hero is indifferent to calling, meaning that the EV of both actions calling or folding is the same. If Villain overbluffs relative to odds laid, Hero can call more than at equilibrium and increase his EV; If Villain underbluffs, hero can fold more than at equilibrium and increase his EV. GTO is all about equilibrium and creating this indifference, which removes the ability for hero to increase his EV through choice of action and thus V cannot be exploited. That is why GTO is often contrasted with exploitative strategies. If you know that you opponent is unbalanced you should exploit that to maximize EV; you cannot exploit a balanced opponent. In these anonymous fast fold games I think GTO is a good choice because generally you know nothing about a specific player so you cannot exploit them. I will say that after over 50k hands at this stake I know that the player pool does have biases that can be exploited; you can only exploit the pool on average but not a specific player if that makes sense.
So based on odds laid, Villain needs to look at her range with which she arrives at a specific spot and break that range into a polarized portion consisting of value bets and bluffs (at a ratio that matches the pot odds laid I think) and a portion of medium strength hands that are checking for an OOP V to X/C if Hero raises or possibly win at showdown if IP Hero checks through.
I'm not super clear on the math here but I think if V is laying 2:1 odds, hero needs to be good 33% of the time at equilibrium. I think that means that V needs 2 bluffs for every 1 value combo in her range in this spot to be balanced. Again I may definitely be wrong on this specific math. So the solver splits the range into a set of value combos, identifies 2 times the number of bluff combos, etc. to build the selections for each entered bet size such that the value/bluff sets of combos are balanced according to the pot odds laid and facing a certain bet Hero with perfect knowledge of V's strategy is indifferent to calling or folding as the EV of both is the same.
So I think in this case, V is jamming this combo 100% of the time in the solve because a) jam is the only bet size I included for river action for V in the solve (V can only jam or check in the solve - but I think that mirrors a real V's choices here) and b) odds laid stipulate a ratio of value hands to bluffs and this hand makes it into the bluff category as it is bottom of range and Villain probably never ever wins by checking given Hero's actions and the strength implied.
This specific combo wouldnt have any chance to fit into the check portion of the range, so strategy is 0% check / 100% jam; with two hearts it unblocks combos in Hero's range that would increase the likelihood that Hero arrived at the river with a busted flush draw. Note that
also jams 100% for the same reason. Both combos are extremely unlikely to win at showdown (maybe less that 0.01% that 6 high is good here given the actions prior) and may be able to get Hero to fold hands that these combos unblock that cant win either like a busted FD.
raising the most at 22%. Maybe as I block some of the draws the solver sees it more likely that this is not a draw raising and V has more value combos?
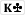
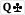calls 100% maybe because it unblocks busted flush draws that would be bluffing? Combos of 77 with a club are only calling 33% as it blocks the busted FD?
and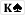 
.
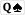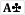
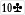calling here 38% of the time?? Maybe because it blocks both 
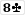and 
