Official Horse Race Game Thread (9 Viewers)

[BSteck]

 

[Tonysquander]

Any warping? The grommets look great, and the board does look a bit higher quality than the pine.

Mine should be here tomorrow. Psyched!

No warp on mine that arrived today. Very nice board and horses.

 

[raynmanas]

No warp on mine that arrived today. Very nice board and horses.

View attachment 891251

#copperhorsesshouldbe2and12

 

[BPTDirector]

Does the pine board come with the fancy cards and felt bag?

It comes with cards and the exact same bag. Just regular cards though.

 

[Sprouty]

We did a side bet of $2 each for the best poker hand after the scratches.

It was fun.

I haven't been through the whole thread yet to see if anyone else is doing that.

 

[raynmanas]

We did a side bet of $2 each for the best poker hand after the scratches.

brilliant, this should be standard.

 

[BSteck]

We did a side bet of $2 each for the best poker hand after the scratches.

It was fun.

I haven't been through the whole thread yet to see if anyone else is doing that.

ooooo!! Or maybe deal out the cards like a game of (11 card?) stud?

 

[raynmanas]

i was wondering what everyone thinks is a good maximum number of players for this game? when we have big get togethers, we love to play LCR with an unlimited number of players for a huge pot, and i'm wondering if this could work as an alternative.

so in theory you could play this game with 44 people, but then 16 would get scratched. so i'm thinking 22 would be a good max, but of course someone could still get scratched, but i think that's fine for the purpose of a big party game.

 

[JeepologyOffroad]

What initial “pay to race” price are you guys playing? $5?

 

[Littleluck55]

I see need for nice dice to complement these beautiful sets! If only there was someone who was making those...

I was ahead of the curve. It’s the reason I ordered dice last year. We’ve been playing this game for years. Love it.

Thanks again @LeGold

 

[BSteck]

What initial “pay to race” price are you guys playing? $5?

None here. The pots are big enough for our crew without the initial ante. Somewhere between 50-100x the base chip.

 

[Littleluck55]

View attachment 891242

Make sure you add some felt to the bottom to keep from scratching your board

 

[Darson]

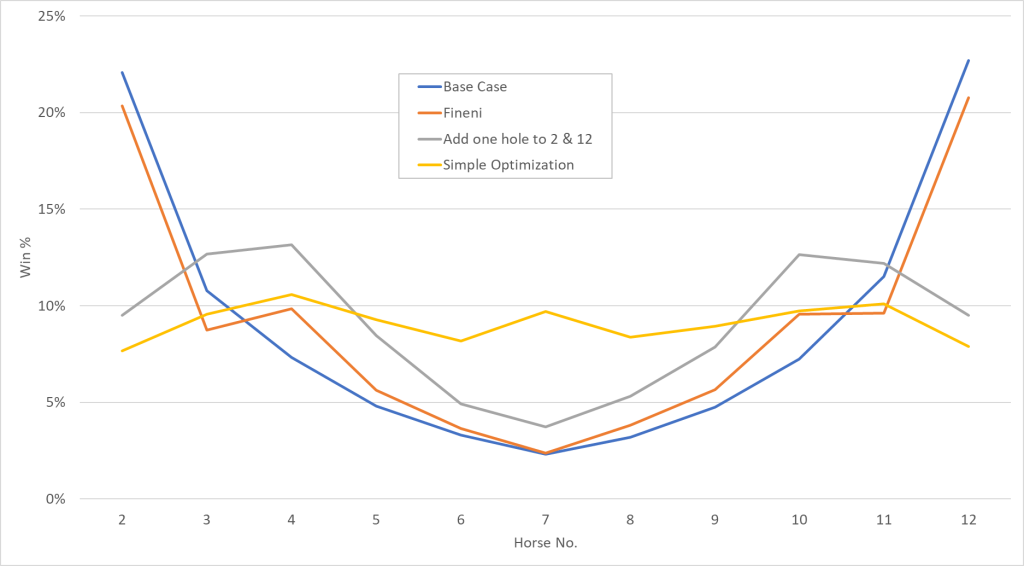
After thinking about win probabilities etc my head would just not be satisfied unless I had the answer while considering the scratched horses. So I wrote a simulation of the game to calculate the probabilities of an individual horse winning. These results are for 10,000 rounds of the game each so not enough for stability but good enough for an idea.

Based on the starting probabilities and the base number of holes to win, here are the win probabilities:

Horse	Win Requirement	Win %
2	3	22%
3	6	11%
4	9	7%
5	12	5%
6	15	3%
7	18	2%
8	15	3%
9	12	5%
10	9	7%
11	6	12%
12	3	23%

Now taking into account the Fineni board with the lower hole counts for horses 4-10:

Horse	Win Requirement	Win %
2	3	20%
3	6	9%
4	8	10%
5	11	6%
6	14	4%
7	17	2%
8	14	4%
9	11	6%
10	8	10%
11	6	10%
12	3	21%

So horses 2 and 12 are much more likely to win.

The simple change of adding a hole to horses 2 and 12 give you these results:

Horse	Win Requirement	Win %
2	4	10%
3	6	13%
4	8	13%
5	11	8%
6	14	5%
7	17	4%
8	14	5%
9	11	8%
10	8	13%
11	6	12%
12	4	10%

And finally a rough optimization to get a tighter spread of win probabilities:

Horse	Win Requirement	Win %
2	4	8%
3	6	10%
4	8	11%
5	10	9%
6	12	8%
7	13	10%
8	12	8%
9	10	9%
10	8	10%
11	6	10%
12	4	8%

However after having run this simulation, I realize that the win% I calculate is considering the final probability of a given horse winning from the start of the game before horses are scratched. So if you want to see a better spread of which horses win over multiple races, the above holes would be better but for a given race, if a middling horse number is not scratched, it'll have a higher chance of winning that race.

And if anyone's interested, here are the probabilities of a given horse being scratched in each of the scratch rounds (taking into account the likelihood of a horse being scratched in a previous scratch round).

Horse	Scratch 1	Scratch 2	Scratch 3	Scratch 4
2	3%	3%	3%	4%
3	5%	6%	6%	7%
4	8%	9%	9%	9%
5	11%	11%	11%	11%
6	14%	14%	13%	13%
7	17%	16%	14%	13%
8	14%	13%	14%	12%
9	11%	11%	11%	11%
10	8%	8%	9%	10%
11	6%	6%	6%	7%
12	3%	3%	3%	4%

 

[Moxie Mike]

The Fineni board uses this scheme, counting the total number of moves needed to cross the finish line:

3, 6, 8, 11, 14, 17, 14, 11, 8, 6, 3

Dividing each of those by the number of times the roll comes up in 36 tosses (1,2,3,4,5,6,5,4,3,2,1) gives:

3, 3, 2.67, 2.75, 2.80, 2.83, 2.80, 2.75, 2.67, 3, 3

Which means that #2, #3, #11, and #12 will be the least likely to win, since they have to move more multiples of their average number of times rolled (3 multiples) than the other horses do (slightly less than 3 multiples).

However, this only counts how likely they are to win versus the other horses before the race starts but after the scratches have been rolled. If you just count how likely each horse is to win overall, then the outside horses will win much more often than the inside horses (#6, #7, #8) because the inside horses get scratched much more often than the outside horses do. Adding a few holes to the outside horses will not be enough to offset their massive advantage in only rarely getting scratched.

But like I said elsewhere, it doesn't really matter how often each horse wins, since every player has an equal chance to win no matter what the horses do.

Thanks on behalf of everyone incapable or too lazy to do the math

 

[CrazyEddie]

After thinking about win probabilities etc my head would just not be satisfied unless I had the answer while considering the scratched horses. So I wrote a simulation of the game to calculate the probabilities of an individual horse winning. These results are for 10,000 rounds of the game each so not enough for stability but good enough for an idea.

 

[Moxie Mike]

After thinking about win probabilities etc my head would just not be satisfied unless I had the answer while considering the scratched horses. So I wrote a simulation of the game to calculate the probabilities of an individual horse winning. These results are for 10,000 rounds of the game each so not enough for stability but good enough for an idea.

Based on the starting probabilities and the base number of holes to win, here are the win probabilities:

Horse	Win Requirement	Win %
2	3	22%
3	6	11%
4	9	7%
5	12	5%
6	15	3%
7	18	2%
8	15	3%
9	12	5%
10	9	7%
11	6	12%
12	3	23%

Now taking into account the Fineni board with the lower hole counts for horses 4-10:

Horse	Win Requirement	Win %
2	3	20%
3	6	9%
4	8	10%
5	11	6%
6	14	4%
7	17	2%
8	14	4%
9	11	6%
10	8	10%
11	6	10%
12	3	21%

So horses 2 and 12 are much more likely to win.

The simple change of adding a hole to horses 2 and 12 give you these results:

Horse	Win Requirement	Win %
2	4	10%
3	6	13%
4	8	13%
5	11	8%
6	14	5%
7	17	4%
8	14	5%
9	11	8%
10	8	13%
11	6	12%
12	4	10%

And finally a rough optimization to get a tighter spread of win probabilities:

Horse	Win Requirement	Win %
2	4	8%
3	6	10%
4	8	11%
5	10	9%
6	12	8%
7	13	10%
8	12	8%
9	10	9%
10	8	10%
11	6	10%
12	4	8%

However after having run this simulation, I realize that the win% I calculate is considering the final probability of a given horse winning from the start of the game before horses are scratched. So if you want to see a better spread of which horses win over multiple races, the above holes would be better but for a given race, if a middling horse number is not scratched, it'll have a higher chance of winning that race.

View attachment 891348

And if anyone's interested, here are the probabilities of a given horse being scratched in each of the scratch rounds (taking into account the likelihood of a horse being scratched in a previous scratch round).

Horse	Scratch 1	Scratch 2	Scratch 3	Scratch 4
2	3%	3%	3%	4%
3	5%	6%	6%	7%
4	8%	9%	9%	9%
5	11%	11%	11%	11%
6	14%	14%	13%	13%
7	17%	16%	14%	13%
8	14%	13%	14%	12%
9	11%	11%	11%	11%
10	8%	8%	9%	10%
11	6%	6%	6%	7%
12	3%	3%	3%	4%

Nicely done. A few questions:

1) I agree 10,000 is a small sample size. What would be more appropriate to get a true representation? 1mm? What would it take to simulate 1 million trials?

2) Why does the probability that a 6, 7 or 8 will be scratched decrease in subsequent scratch rounds? Is this taking in the likelihood that that horse will have been scratched in previous rounds? If so, could it be adjusted so that isn't factored in?

3) About the last section, what is the probability of a given horse being scratched in ANY of the 4 scratch rounds?

4) When I drilled the holes for my board, I went off the layout from the boards from Across The Board Horse Racing - whom unless I am mistaken are the originators of the game. Their numbers (to win) are 3/6/8/11/14/17. Would it be possible to run your simulation with those numbers?

 

[TheOffalo]

4) When I drilled the holes for my board, I went off the layout from the boards from Across The Board Horse Racing - whom unless I am mistaken are the originators of the game. Their numbers (to win) are 3/6/8/11/14/17. Would it be possible to run your simulation with those numbers?

The ATB and FINENI boards have the same numbers of holes.

Now taking into account the Fineni board with the lower hole counts for horses 4-10:

Horse	Win Requirement	Win %
2	3	20%
3	6	9%
4	8	10%
5	11	6%
6	14	4%
7	17	2%
8	14	4%
9	11	6%
10	8	10%
11	6	10%
12	3	21%

So horses 2 and 12 are much more likely to win.

 

[Darson]

Nicely done. A few questions:

1) I agree 10,000 is a small sample size. What would be more appropriate to get a true representation? 1mm? What would it take to simulate 1 million trials?

2) Why does the probability that a 6, 7 or 8 will be scratched decrease in subsequent scratch rounds? Is this taking in the likelihood that that horse will have been scratched in previous rounds? If so, could it be adjusted so that isn't factored in?

3) About the last section, what is the probability of a given horse being scratched in ANY of the 4 scratch rounds?

4) When I drilled the holes for my board, I went off the layout from the boards from Across The Board Horse Racing - whom unless I am mistaken are the originators of the game. Their numbers (to win) are 3/6/8/11/14/17. Would it be possible to run your simulation with those numbers?

1) Time is all that's required for 1 million sims, it only takes a few minutes (and my code is far from optimal) - I ran it last night with the Fineni/ATB hole pattern:

Horse	Scratch 1	Scratch 2	Scratch 3	Scratch 4	Winner
2	2.8%	3.1%	3.4%	3.8%	20.3%
3	5.6%	6.0%	6.4%	7.0%	9.5%
4	8.2%	8.7%	9.0%	9.4%	9.7%
5	11.0%	11.2%	11.2%	11.1%	5.6%
6	14.0%	13.4%	12.8%	12.2%	3.6%
7	16.7%	15.5%	14.2%	12.9%	2.5%
8	13.9%	13.5%	13.1%	12.4%	3.6%
9	11.2%	11.2%	11.1%	11.0%	5.7%
10	8.3%	8.6%	9.0%	9.5%	9.6%
11	5.6%	5.9%	6.5%	6.9%	9.5%
12	2.9%	3.1%	3.5%	3.9%	20.2%

2) Yes, the subsequent round scratch probabilities take into consideration the likelihood of being scratched in a previous round. This is why the scratch probability decreases for the middle horses (they are more likely to have been scratched in a previous round) and increases for the peripheral horses (there are less horses to choose from so the likelihood of being scratched increases). And for the 5 and 9 horse the decrease due to the likelihood of being scratched in a previous round is almost entirely offset by the increase due to the lower number of horses in subsequent rounds.

3) Probability of a horse being scratched in any of the 4 rounds:

Horse	Scratch Any
2	3.3%
3	6.2%
4	8.8%
5	11.1%
6	13.1%
7	14.8%
8	13.2%
9	11.1%
10	8.8%
11	6.2%
12	3.3%

 

[legonick]

1) Time is all that's required for 1 million sims, it only takes a few minutes (and my code is far from optimal) - I ran it last night with the Fineni/ATB hole pattern:

Horse	Scratch 1	Scratch 2	Scratch 3	Scratch 4	Winner
2	2.8%	3.1%	3.4%	3.8%	20.3%
3	5.6%	6.0%	6.4%	7.0%	9.5%
4	8.2%	8.7%	9.0%	9.4%	9.7%
5	11.0%	11.2%	11.2%	11.1%	5.6%
6	14.0%	13.4%	12.8%	12.2%	3.6%
7	16.7%	15.5%	14.2%	12.9%	2.5%
8	13.9%	13.5%	13.1%	12.4%	3.6%
9	11.2%	11.2%	11.1%	11.0%	5.7%
10	8.3%	8.6%	9.0%	9.5%	9.6%
11	5.6%	5.9%	6.5%	6.9%	9.5%
12	2.9%	3.1%	3.5%	3.9%	20.2%

View attachment 891530

2) Yes, the subsequent round scratch probabilities take into consideration the likelihood of being scratched in a previous round. This is why the scratch probability decreases for the middle horses (they are more likely to have been scratched in a previous round) and increases for the peripheral horses (there are less horses to choose from so the likelihood of being scratched increases). And for the 5 and 9 horse the decrease due to the likelihood of being scratched in a previous round is almost entirely offset by the increase due to the lower number of horses in subsequent rounds.

3) Probability of a horse being scratched in any of the 4 rounds:

Horse	Scratch Any
2	3.3%
3	6.2%
4	8.8%
5	11.1%
6	13.1%
7	14.8%
8	13.2%
9	11.1%
10	8.8%
11	6.2%
12	3.3%

My apologies if you already answered this, but with your first table, does the "win %" include the "scratch %" (in that scratched horses can't win) or it stands alone as in doesn't take scratching into consideration?

 

[Darson]

If you're building your own board, I would recommend the following hole pattern as an easy to remember distribution:

Horse	Win (number of jumps to win)	Win %	Number of peg holes between start and finish
2	4	8%	3
3	6	10%	5
4	8	10%	7
5	10	9%	9
6	12	8%	11
7	14	8%	13
8	12	8%	11
9	10	10%	9
10	8	10%	7
11	6	10%	5
12	4	8%	3

We have played this game a total of about 8 hours now and the 2/12 horses win about 50% of the time. Not sure if others have experienced this but those horses shouldn’t be winning that much. If the 7 horse doesn’t scratch, it hardly ever wins.

To round this out - your estimate is very close! The likelihood of a 2/12 horse winning is just over 40%. Adding just one hole to the 2 & 12 horse drops this to 20% which is probably the ideal minimal intervention solution. The average over the 11 horses should be about 9%

My apologies if you already answered this, but with your first table, does the "win %" include the "scratch %" (in that scratched horses can't win) or it stands alone as in doesn't take scratching into consideration?

The win% is the result from the simulation. It's how many times that horse won over a million rounds of the game. So it intrinsically includes the impact of the scratch phase.

 

[NotDunric]

Hello there!

Direct from ATB. A couple of the rubber bumpers came off the bottom of the board during packing/shipping (found one in the box loose, the other is MIA), but otherwise board is in great shape. Can’t wait to introduce this to more of my groups!

e: Oh! Also confirmed that chips racks (Chipcos in my testing) fit comfortably inside these larger ATB boards with the flip-open compartment, so something to consider for future shoppers!

 

[Venturalvn]

Hello there!
View attachment 891588

Direct from ATB. A couple of the rubber bumpers came off the bottom of the board during packing/shipping (found one in the box loose, the other is MIA), but otherwise board is in great shape. Can’t wait to introduce this to more of my groups!

e: Oh! Also confirmed that chips racks (Chipcos in my testing) fit comfortably inside these larger ATB boards with the flip-open compartment, so something to consider for future shoppers!

That sure is a pretty board

 

[chrismurda]

Haven’t hosted my regular game since pre pandemic which was before my chipping journey… they are in for a surprise.

Edited to add photo with better lighting.

 

[DoubleEagle]

Getting a board. However after reading this entire thread, I’m not sure which board to get. I am leaning toward the ATB since it comes as box with the game board opening as the lid with storage under the game board.

Fineni (Cherry)
ATB (Walnut box with lid)

Which one and why?

 

[BPTDirector]

Getting a board. However after reading this entire thread, I’m not sure which board to get. I am leaning toward the ATB since it comes as box with the game board opening as the lid with storage under the game board.

Finei (Cherry)
ATB (Walnut box with lid)

Which one and why?

Both of these are top notch solid choices. The ATB because of the box as you mention, the FINENI because of the premium horses. Can’t go wrong. I have the FINENI and will have a box made to fold in half with felt lining so the top can be used to toss the dice into.

 

[legonick]

Haven’t hosted my regular game since pre pandemic which was before my chipping journey… they are in for a surprise.

Edited to add photo with better lighting.
View attachment 891744View attachment 891745

Any details on those chips? Those are bangin'! I love the colors on the $1, $5, and $20, and the cool like GTA Vice City vibe (80s Miami).

 

[legonick]

Getting a board. However after reading this entire thread, I’m not sure which board to get. I am leaning toward the ATB since it comes as box with the game board opening as the lid with storage under the game board.

Fineni (Cherry)
ATB (Walnut box with lid)

Which one and why?

Tough call. Assuming no mod.s being made, I think for you it'll come down to, do you want the box/storage stuff, or the better "finish" and horses (Fineni board stuff is painted not stickers, so I suspect it will last "forever" where as the stickers could eventually dry out and peel off, although I'm sure it could take a long long time for that to happen...and also, the multi-colored more "premium" 3D horses VS the "flat" horses of the ATB set).

 

[chrismurda]

Any details on those chips? Those are bangin'! I love the colors on the $1, $5, and $20, and the cool like GTA Vice City vibe (80s Miami).

Tribute set for my daughter, Summer. Inlay by @timinater dice by @LeGold and chips by many. I made an alternate set for higher limit degen nights which can be here: Summer Resort & Casino

 

[DoubleEagle]

Getting a board. However after reading this entire thread, I’m not sure which board to get. I am leaning toward the ATB since it comes as box with the game board opening as the lid with storage under the game board.

Fineni (Cherry)
ATB (Walnut box with lid)

Which one and why?

I decided to go with the Fineni for the painted on graphics and nicer horses. Really like the idea of the box though. Maybe @Darson will start a new business!

 

[NotDunric]

Does anyone with a Fineni board have the ability to measure their board's grommets or the pegs on their horses? I do love their nicer horses, curious if they'd fit into my ATB setup.